The physical properties of gases are very simple and identical for all gases. These properties of different gases are evident from the fact that all gases generally obey some simple or common gas formula or relation. Boyle's law, Charles law, Avogadro law, Gay Lussac law, ideal gas law, and Graham's law provide the relation between mass, pressure, volume, temperature, and density of ideal gas molecules for learning chemistry or physics. After knowing these experimental ideal gas laws, a theoretical model-based structure of gases was developed in kinetic theory.
Eventually, these individual laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures. We will consider the key developments in individual relationships , then put them together in the ideal gas law. Avogadro's Number, the ideal gas constant, and both Boyle's and Charles' laws combine to describe a theoretical ideal gas in which all particle collisions are absolutely equal. The laws come very close to describing the behavior of most gases, but there are very tiny mathematical deviations due to differences in actual particle size and tiny intermolecular forces in real gases.
Nevertheless, these important laws are often combined into one equation known as the ideal gas law. Using this law, you can find the value of any of the other variables — pressure, volume, number or temperature — if you know the value of the other three. The behavior of gases can be described by several laws based on experimental observations of their properties. The pressure of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does not change (Amontons's law). The volume of a given gas sample is directly proportional to its absolute temperature at constant pressure (Charles's law).
The volume of a given amount of gas is inversely proportional to its pressure when temperature is held constant (Boyle's law). Under the same conditions of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro's law). This is Avogadro's law, which states that under the same temperature and pressure, equal volumes of all gases contain the same number of molecules.
This equation shows that if the quantity of gas increases, the volume of gas increases proportionally. In other words, the number of gas atoms or molecules is independent of their sizes or the molar mass of the gas. The law is named after an Italian scientist Amedeo Avogadro who published his hypothesis about the relationship between the gas volume and its amount in moles in 1811. The standard fixed point of the absolute temperature scale is known as the triple point of water. The significance of this point can be seen in Figure 13, which shows some of the conditions of temperature and pressure under which a fixed quantity of water will exist as a solid , a liquid or a gas . Notice that the graph shows low pressures, around 1% of normal atmospheric pressure.
But you can also see that the melting temperature, at which water makes the transition from solid to liquid, increases slightly as the pressure falls. As a consequence, the two lines meet at a temperature of 0.01 °C when the pressure is 600 Pa. Under these unique conditions water vapour, liquid water and solid ice can all coexist in equilibrium. You can use values for real gases so long as they act like ideal gases. To use the formula for a real gas, it must be at low pressure and low temperature. Increasing pressure or temperature raises the kinetic energy of the gas and forces the molecules to interact.
While the ideal gas law can still offer an approximation under these conditions, it becomes less accurate when molecules are close together and excited. Boyle's law asserts that when the temperature of a fixed quantity of gas is held constant, the product of its pressure and volume is constant. Charles' law asserts that when the pressure of a fixed quantity of gas is held constant, the volume is proportional to the quantity (Tcen + 273° centigrade), where Tcen is the centigrade temperature. This suggests that there exists a lowest possible temperature, usually called absolute zero, at about −273° centigrade.
How Do You Find The Volume Of A Gas Given Temperature Gases whose properties of P, V, and T are accurately described by the ideal gas law are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter. Although all the calculations presented in this module assume ideal behavior, this assumption is only reasonable for gases under conditions of relatively low pressure and high temperature. In the final module of this chapter, a modified gas law will be introduced that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures. First, we must determine the question, which is to calculate the volume of a quantity of gas at a given temperature and pressure.
In a second step, after establishing a basis, we must convert the mass of methane that will be the basis into pound moles. Third, we must convert temperature in degrees Fahrenheit into absolute degrees Rankin and, fourth, convert pressure from psig into psia. Fifth, we must select the appropriate ideal gas constant and use it with a rewritten form of Equation 4.11 to determine the volume of 11.0 lbs of methane gas. Finally, we can substitute the values previously determined into the rewritten equation to calculate the volume. An ideal, or perfect, gas is a hypothetical gas that obeys the gas laws in terms of its pressure, volume, and temperature behavior.
Such a gas would have to be composed of molecules that do not interact with one another. Real gases are not always accurately described by the ideal gas equation. Under ordinary conditions, however, the observed behavior of a real gas is only negligibly different from that predicted for an ideal gas. The compressibility factor is a useful thermodynamic property for modifying the ideal gas law to account for behavior of real gases. It is a measure of how much the thermodynamic properties of a real gas deviate from those expected of an ideal gas. It may be thought of as the ratio of the actual volume of a real gas to the volume predicted by the ideal gas at the same temperature and pressure as the actual volume.
The attraction or repulsion between the individual gas molecules and the container are negligible. Further, for an ideal gas, the molecules are considered to be perfectly elastic and there is no internal energy loss resulting from collision between the molecules. Such ideal gases are said to obey several classical equations such as the Boyle's law, Charles's law and the ideal gas equation or the perfect gas equation. We will first discuss the behavior of ideal gases and then follow it up with the behavior of real gases. But something happens to the validity of this assumption as the gas is compressed.
Imagine for the moment that the atoms or molecules in a gas were all clustered in one corner of a cylinder, as shown in the figure below. At normal pressures, the volume occupied by these particles is a negligibly small fraction of the total volume of the gas. As a result, real gases are not as compressible at high pressures as an ideal gas. The volume of a real gas is therefore larger than expected from the ideal gas equation at high pressures.
This relationship between temperature and pressure is observed for any sample of gas confined to a constant volume. An example of experimental pressure-temperature data is shown for a sample of air under these conditions in . An example of experimental pressure-temperature data is shown for a sample of air under these conditions in Figure 9.11. Careful experiments show that the ideal gas laws are only approximately obeyed by different gases. The ideal gas equation can be used to distinguish between ideal gas and real gas.
The gas which obeys this equation is called ideal gas and which does not obey this equation is called real gas. Van der Waals equation was used to derive the properties of real gases. The ideal gas law formula states that pressure multiplied by volume is equal to moles times the universal gas constant times temperature.
The properties of gases were already being studied and described as early as the seventeenth century. Unlike solids, which have a fixed shape and volume, and liquids, which have a fixed volume but can change shape according to the container, gases assume both the shape and the volume of their container. The volume of space occupied by a sample of gas depends on the number of gas molecules present and the sample's pressure and temperature. The relationship between pressure and temperature of a gas is stated by Gay-Lussac's pressure temperature law. This law states that the pressure of a fixed mass of gas held at a constant volume is directionally proportional to its Kelvin temperature .
Therefore, as the pressure of a particular system goes up, the temperature of that system also goes up, and vice versa. Gas laws describe the behavior of gases with respect to the pressure, volume, temperature, and amount. Gases are one of the states of matter, either compressed very tightly or expanded to fill a large space. There is a useful idealization of gas behaviour which can be formally defined as that in which Boyle's law is exactly true for all temperatures and pressures. A gas which behaves in this way is called an ideal gas and although it is an idealization, real gases approach it under certain conditions.
There are two reasons why it is useful to formulate the equations that an ideal gas would obey. First, these equations are simple and provide a valuable 'first approximation' to the equations that describe real gases. Second, the deviations from ideal gas behaviour that real gases exhibit can give us insight into the microscopic properties of real gases.
Much like the combined gas law, the ideal gas law is also an amalgamation of four different gas laws. Here,Avogadro's law is added and the combined gas law is converted into the ideal gas law. This law relates four different variables which are pressure, volume, no of moles or molecules and temperature. Basically, the ideal gas law gives the relationship between these above four different variables. Constant into the ideal gas equation that was equal to the volume actually occupied by a mole of gas particles. Because the volume of the gas particles depends on the number of moles of gas in the container, the term that is subtracted from the real volume of the gas is equal to the number of moles of gas times b.
While ideal gases are strictly a theoretical conception, real gases can behave ideally under certain conditions. Similarly, high-temperature systems allow for the gas particles to move quickly within the system and exhibit less intermolecular forces with each other. Therefore, for calculation purposes, real gases can be considered "ideal" in either low pressure or high-temperature systems. We have just seen that the volume of a specified amount of a gas at constant pressure is proportional to the absolute temperature. In addition, we saw that the volume of a specified amount gas at a constant temperature is also inversely proportional to its pressure.
We can correctly assume that pressure of a specified amount of gas at a constant volume is proportional to its absolute temperature. Let us also add the fact that the volume at constant pressure and temperature is also proportional to the amount of gas. Similarly, the pressure at constant volume and temperature is proportional to the amount of gas. Thus, these laws and relationships can be combined to give Equation 4.10. The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure of 1 atm. If the temperature is in kelvin, volume and temperature are directly proportional.
Charles's law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant. Plotting the pressure against the absolute temperature gives a straight line which when extrapolated passes through the origin. This shows the pressure of the gas is directly proportional to the absolute temperature of the gas. Doubling the temperature will double the pressure for a fixed mass of gas at constant volume. It also shows that if the gas is cooled to absolute zero then the energy of the molecules is at the lowest energy state and therefore cannot generate any pressure.
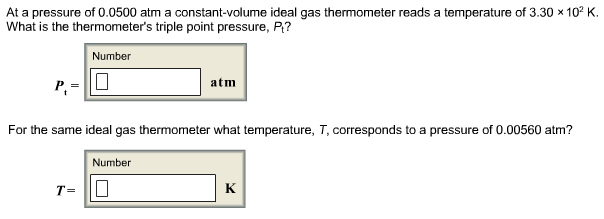
So, provided we work at low pressures with a constant–volume gas thermometer, the nature of the working substance is of little relevance. Boyle's law states, at a constant temperature, the volume of a definite mass of a gas is inversely proportional to its pressure. Therefore, the volume of a given quantity of gases, at constant temperature equilibrium with the pressure of gases.
At constant temperature and 1 atm pressure, a cylinder contains 10 ml of methane or hydrogen gas. If the pressure increases to 2 atm then according to Boyle's Law volume decreases to 5 ml. This ideal gas law calculator will help you establish the properties of an ideal gas subject to pressure, temperature, or volume changes.
Read on to learn about the characteristics of an ideal gas, how to use the ideal gas law equation, and the definition of the ideal gas constant. Temperature is sometimes measured with a gas thermometer by observing the change in the volume of the gas as the temperature changes at constant pressure. The hydrogen in a particular hydrogen gas thermometer has a volume of 150.0 cm3 when immersed in a mixture of ice and water (0.00 °C).
When immersed in boiling liquid ammonia, the volume of the hydrogen, at the same pressure, is 131.7 cm3. Find the temperature of boiling ammonia on the kelvin and Celsius scales. The simple and ideal gas laws describe the behavior of pure gaseous substances. Mixtures of gases also behave like ideal gases, provided the different components do not undergo a reaction, or interact in some other way. This concept—that each individual gas in a mixture expands to exert its partial pressure as if the other gas components were not present—was developed by John Dalton in 1801 and is known as Dalton's law of partial pressures.
The volume of space occupied by a sample of gas depends on the number of gas mole-cules present and the sample's pressure and temperature. This is why we have found it necessary to jump backwards and forwards in this module between the basics of thermometry and the properties of gases. Nonetheless, we are now able to define the absolute temperature scale. The behavior of real gases usually agrees with the predictions of the ideal gas equation to within 5% at normal temperatures and pressures.
At low temperatures or high pressures, real gases deviate significantly from ideal gas behavior. The combined gas law is also known as a general gas equation is obtained by combining three gas laws which include Charle's law, Boyle's Law and Gay-Lussac law. The law shows the relationship between temperature, volume and pressure for a fixed quantity of gas.
To first order, pressure ratios are equal to temperature ratios, with thermodynamic temperatures calculated using known virial coefficients. If the constant-volume gas thermometer is to be used in an interpolating gas thermometer mode (as for the ITS-90), the major corrections are due to the nonideality of the gas. The kinetic energy per unit of temperature of one mole of a gas is a constant value, sometimes referred to as the Regnault constant, named after the French chemist Henri Victor Regnault. Regnault studied the thermal properties of matter and discovered that Boyle's law was not perfect.
When the temperature of a substance nears its boiling point, the expansion of the gas particles is not exactly uniform. Decreasing the volume of the container forces the particles to collide more often, so the pressure is increased. As more air goes in, the gas molecules get packed together, reducing their volume. As long as the temperature stays the same, the pressure increases.
According to Charles's law, heating a gas will increase its volume. Also, as noted in the first and second propositions regarding the behavior of gases, gas molecules are highly nonattractive to one another, and therefore, there is a great deal of space between them. The increase in volume makes that space even greater, leading to a significant difference in density between the air in the balloon and the air outside. The major issue with the idea gas law is that it neglects both molecular size and intermolecular attractions, therefore it is most accurate for monatomic gases at high temperatures and low pressures. With lower densities the neglect of molecular size becomes less critical since the average distance between adjacent molecules becomes much larger relative to the size of the molecules themselves.